Howling Banshees or Striking Scorpions

If you have ever played Warhammer 40,000 or even visited the forums devoted to the game, you know that discussion of the day is usually “which unit is better”. Sometimes this is just plain ePenis wagging, bragging and blustering – but sometimes these debates have tactical and monetary merits. Especially when the parties involved in the discussion play the same army, and are arguing about effectiveness of certain units, and therefore their overall worth to you as a player. Warhammer miniatures cost real world money, and take time and effort to paint. A bad unit selection can set you back quite a bit.

Of course if you love the hobby and enjoy painting and converting, this is not a big deal. Even if you won’t field the unit in many battles, it will still look cool on your shelf as a display piece. But if you are putting together an army for tournament play for example, things like effectiveness matter.

Personally, I’m an Eldar player. For those of you who don’t know much about the game Eldar are essentially space elves. They are fast but fragile, and the have a wide range of very specialized, hard hitting, special-purpose units and almost no flexible all-purpose ones. As a result we love to discuss which of these units will fare the best under the most common set of battle scenarios. The most heated discussion usually involves close combat units.

Eldar are not great in melee. They are decent, and can cut through weaker foes, but often struggle facing elites. Space Marines – heavily armored super soldiers can usually mop the floor with your average Eldar unit unless you get a jump on them. And it just so happens that Marines are the most popular type of army out there. At an average tournament, chances are that 80% of players you face will play some flavor of marines – either vanilla, one of the four specialized chapters with their own special rules and disadvantages, or Chaos Space Marines (the evil flavor). So picking a close combat unit that can stand up to Marines is an important strategic decision.

Eldar have two main close combat specialist squads: Howling Banshees and Striking Scorpions. Banshees are usually thought of as the designated anti-Marine choice. They wield “power weapons” – energized can openers that ignore the impenetrable Marine armor which lets them shrug off over 60% of incurred damage. Unfortunately they are rather lightly armored, and do not pack enough punch to actually hurt the marines too badly, which makes them slightly less than imposing.

Howling Banshees

Striking Scorpions on the other hand are about a match for marines in terms of raw strength and punch-out force. They wear heavier armor which gives them more staying power, and they can score more attacks per round (up to 30 in perfect conditions at max size compared to up to 20 for a Banshee unit in the same circumstances). What they do not have, is Banshee ability to crack open Space Marine armor, which means a large number of their attacks will harmlessly bounce of of it.

Striking Scorpions

You can probably see the dilemma here – what’s more effective: the ability to score a lot of wounds, many of which will be deflected, or the ability to score a few wounds but make them count. Many Eldar players have strong opinions one way or the other. Some skirt around the issue and just field both units in every battle (oh, Biel-Tan, when will you ever learn). As far as I know, no one has really made any statistical analysis on this subject. Most of what you read online is anecdotal evidence – stories of players who had particular luck against marines using either Banshees or Scorpions – or theoretical discussions of probability distributions for each unit.

I figured that the only way to settle this dispute once and for all, is to set up an experiment. Lets pit a unit of Scorpions and a unit of Banshees against your average Space Marine squad. Let’s roll the dice, record the results and see which one managed to kill more marines while loosing the least troops. Then let’s repeat it over and over and over again until we have a viable statistical sample. Let’s say 100,000 rounds should do the trick.

Methodology

Conducting such experiment using real models and real dice would be silly. I opted to simulate them in software. I wrote a small Python script (a little over 150 lines) that would emulate the first round of combat between an Eldar and Marine unit using the following assumptions:

1. Both Eldar units fight against standard Space Marine Tactical Squad – not an Assault Squad. I figured tacticals are more common.
2. Neither Eldar or Marine unit have any upgrades. This means no Exarchs, no powers, no sergeants, no special weapons and etc.
3. The combat takes place on flat field, and the units line up perfectly – every model in base contact with an enemy. This means all attacks go in, there are no cover bonuses and etc..
4. Eldar get to strike first due to their higher initiative
5. Eldar and Marines are more or less matched when it comes to weapon skill so they always hit on 4 or more
6. Banshees have two attacks each, and need a 5 to wound. Scorpions have three attacks and need only a 4.
7. Marines forgo saves against Bashees but get the usual 3+ protection against the scorpions
8. When Marines strike back they need only a 3 to wound. Banshees save on 4, Scorpions on 3.

I’m simulating dice rolls using the standard python method – using the random library like so:

def roll(over):
	i = random.randint(1,6)
	return (i>=over)

You can see the entire script on Github. I’m not going to copy and paste it here, because it’s to long:

• eldar.py

Please note that I am only simulating the first round of combat during which Eldar have the biggest advantage. While a melee between Marines and Eldar will often last several turns, the first round is usually very important. Scoring enough wounds right of the get-go can cripple the opponents ability to deal damage later on, and even if they win in the end, it may render their unit unusable for purposes such as capturing objectives.

I figured that showing how each of the units will fare in their first round will be enough to judge their overall effectiveness.

When judging the results, I do it the way you would normally resolve a round: I compare how many unsaved wounds was scored on both sides. If Eldar scored more wounds than they incurred casualties then they win the round. If both sides score the same, its a tie. Otherwise Marines win.

Results

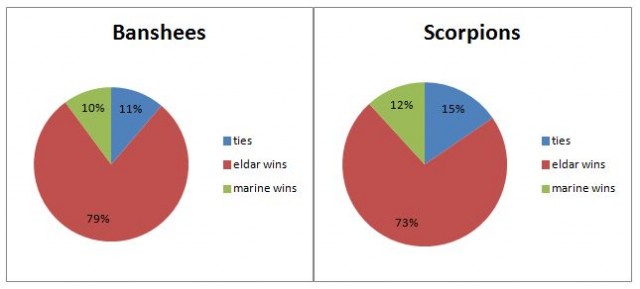
When I started running this experiment, I expected to see a large skew in favor of either Banshees or the Scorpions. Because of all the heated discussions about their effectiveness I witnessed over the years I wanted to see one or the other side of the argument validated. Unfortunately, it seems that both units are remarkably balanced. After 100,000 rounds here is the overall spread of wins, losses and ties:

Banshees vs Scorpions

Over 100,000 runs, Banshees won a round only 6% more often than Scorpions. On the other hand Scorpions tied a little bit more often – most likely due to their superior armor. The difference between the two units it is almost insignificant at this scale. Both units are quite adept at dominating the enemy on the first round, but neither one seems to be better at it than the other. Lets delve a little bit deeper and see some more statistical data on this simulation:

Banshees vs Scorpions Statistical Detail

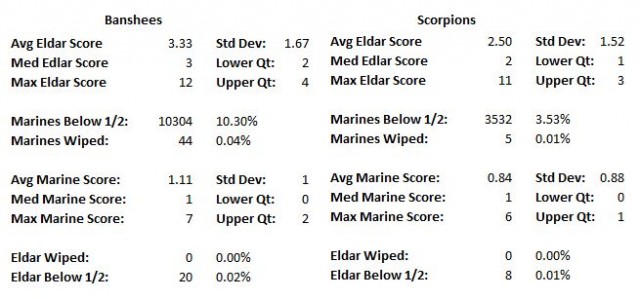
Over the 100,000 trials both units killed on average between 2-3 Marines. Banshees killed a little bit more efficiently (nearing almost 4 marines on average, 3 being the median score) with scorpions averaging a little below 3 (2 median). Looking at that data alone, you could summarize that the brute strength and ferocity of Scorpion attack is essentially a perfect match of the Banshee can opening skills. Or rather, in the long run Marine armor is not as effective as one would think.

I expected Scorpions to incur significantly less casualties due to their heavy armor, but surprisingly this turned out not to matter all that much. Both units lost on average one man in the first turn showing that the Scorpions do not have a huge advantage over the Banshees in this department.

Banshees did show a slight edge in their ability to bring down the Marine unit below half strength on the first turn. They have accomplished this feat roughly 10% of the time, to Scorpions measly 3%. Of course, both cases are rather statistically insignificant. Most rounds ended in a close victory for the Eldar, but with Marine unit still over half strength. The rounds in which Eldar stomped the Marines into the ground, eradicating the entire squad were extremely rare – 44 occurrences for Banshees and 5 for Scorpions.

I urge you not to take my word for this. You can find my data sets on Github alongside the code. They are tab-separated text files that can be easily imported into Excel, or parsed with awk/sed for further analysis:

• Banshees data dump
• Scorpions data dump

Here is the clarification for the headers:

eh = eldar hits
ew = eldar wounds
mh = marine hits
mw = marine wounds
de = dead eldar
dm = dead marines

Summaries are underneath the raw data. You can use these files to run more in depth analysis than me. Also feel free to inspect the code, correct any mistakes you see and run such experiment on your own.

I have ran this 100,000 round test several times to make sure the numbers I got were not a fluke. Remarkably the ratio of wins to losses remained almost the same on subsequent runs.

Based on the statistical data I can conclude that there is virtually no tactical advantage in using Banshees over Scorpions. Both units are equally effective at fighting Marines. In fact, these results suggest that Scorpions are a more well rounded choice for tournament play. While they are about equal to Banshees in effectiveness against Marines they do have superior strength and armor making them much more dangerous to less armored opponents. While Banshees specialize in cracking open Marine power armors they do not pack enough punch to do well against lightly armored, ferocious melee fighters.

Further Research

This experiment was rather limited by the scope. For one, it only looked at the first round of combat – mostly to keep things simple. While in many cases first round tends to be decisive, I have witnessed enough nearly miraculous third or fourth turn come-backs to completely discard them. To get a full picture, it would be worth while to extend the python script to simulate entire combat sequence – from start to a failed moral e check or annihilation.

In addition, part of the Eldar Aspect Warrior effectiveness stems from their Exarchs – an upgraded unit leaders, who can use more powerful weapons and bestow a range of special effects on their unit. It is likely that combination of weapons and Exarch powers could easily skew the balance toward either Banshees or Scorpions.

Perhaps I will investigate these things in another post.